Reinforcement Learning
Reinforcement Learning
- Use reinforcement learning is when it is hard to provide a training set
- E.g. situation-action pairs
Framework
- An agent interacts with its environment.
- There is a set $S$ of states, set $A$ of actions
- At each time t, agent is at a state $s_t$, must choose an action $a_t$
- Goes into state $s_{t+1}=\delta(s_t,a_t)$
- Receives a reward $r_t = R(s_t,a_t)$
- Agent has a policy $\pi:S\rightarrow A$, and the aim is to find an optimal policy $\pi^*$ that maximises the cumulative reward
- $\delta, R, \pi$ can be multi-valued with random element (e.g. can be treated as probability distributions)
Models of Optimality
| Reward | Cumulative reward | Comment |
|---|---|---|
| Finite horizon reward | $\sum_{i=0}^{h-1} r_{t+i}$ | Simple computationally |
| Infinite discounted reward | $\sum_{i=0}^\infty\gamma^ir_{t+i}$ | Easier for proving theorems |
| Average reward | $lim_{h\rightarrow \infty}\frac{1}{h}\sum_{i=0}^{h-1}r_{t+i}$ | Cannot sensibly choose between small reward soon and large reward later |
- Various ways of learning, based on:
- Value Function Learning, e.g. TD-, Q-Learning
- Policy Learning, e.g. Hill Climbing, Policy Gradients
- Actor-Critic, a mix of both
Value Function Learning
Each policy $\pi$ has a value function $V^\pi:S\rightarrow R$ where $V^\pi(s)$ is the average discounted reward received by agent who starts at s and chooses actions according to $\pi$
Average discounted reward - rewards arriving later in the future are worth less - controls how far the agent looks ahead when making predictions.
The agent retains its own estimate of $V^*$, the maximum (expected) discounted reward. The aim is to start with a random V and improve it until it is close to V* (bootstrapping).
Exploration vs. Exploitation
- Either choose a random action or choose what we think is the best action
- choose a random action 5% of the time, or
- use Softmax (Boltzmann distribution) to choose next action:
$P(a) = \frac{e^{R(a)/T}}{\sum_{b\in A}e^{R(b)/T}}$
TD-Learning
- For the true value $V^*(s)$, it is equal to the immediate reward plus discounted value of the next state:
$V^*(s)=R(s,a)+\gamma V^*(\delta(s,a))$
- For the estimated value, we want to learn - so incorporate the error and learning rate:

Q-Learning
- Q-Learning is similar but depends on a state-action pair, not just a state. Done via the function $Q^\pi : S \times A \rightarrow R$ in place of the value function.
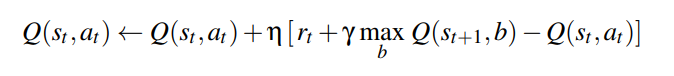
- Limitations:
- Delayed reinforcement: rewards might not be received until several time steps after - slows down learning
- Search space must be finite - relies on visiting every state infinitely often
- Real world problems cannot rely on lookup table (we are looking up the reward for a particular state or state-action) - need to generalise
Backprop
- Supervised learning:
- Learn from human games
- TD-Learning
- Use subsequent positions to refine evaluation of current position
- General method that does not rely on world model, e.g. the rules of the game
- TD Learning and backprop
Policy Learning
- Attempt to optimise the policy $\pi_\theta : S\rightarrow A$ directly, with parameters $\theta$
- We consider the fitness of a policy as the value function of initial state under that policy
$fitness(\pi_\theta) = V^{\pi_\theta}(s_0)=E_{\pi_\theta}(r_{total})$
Evolution Strategy
- Hill climbing
- Initialise a ‘champ’ policy $\theta_{champ} = 0$
- For each trial, generate a mutant policy $\theta_{mutant} = \theta_{champ} + Gaussian\space noise$
- Evaluate both on same task, if mutant is better then $\theta_{champ}\leftarrow (1-\alpha)\theta_{champ} + \alpha\theta_{mutant}$
Policy Gradients
- Use gradient ascent instead of random updates. For episodic:
- After a sequence of actions, we receive a total reward - distribute reward to each action equally
- If total reward is high, we change parameters to make agent more likely to take those actions in similar situations, e.g. we want to increase the total reward: $log\prod_{t=1}^m \pi_\theta (a_t|s_t)$
- This is the REINFORCE algorithm:

- For non-episodic, rewards are received incrementally throughout the game - policy is a probability distribution

Actor-Critic
- For the above fitness gradient, it is hard to estimate the Q value. Actor-Critic:
- Critic NN measures how good the action taken is (value-based)
- Have a family of Q functions and learn different parameters to approximate $Q^{\pi_\theta}$
- Actor NN controls how our agent behaves (policy-based)
- At the same time as approximating $Q^{\pi_\theta}$, we are learning the best policy
- Instead of updating eery episode in REINFORCE, we update every step (e.g. like in TD Learning)
