Image Processing
Image Processing
Image Datasets and Tasks
- Various datasets:
- MNIST handwritten digits, 10 classes, 6000 each
- CIFAR colour images, 10 classes, 5000 each
- ImageNet LSVRC - more images
- Tasks:
- image captioning
- image classification
- object detection
- object segmentation
- generating images
- generating art
- style transfer
AlexNet
- Enhanced using: ReLUs, overlapping pooling, stochastic gradient descent with momentum and weight decay, 50% dropout in fully connected layers
- Data augmentation
- Cropping out 10 patches of the original image
- Horizontal reflection of each patch included
- RGB channels had changed intensities
- Predictions of the 10 patches averaged at testing
- Convolution Kernels
- Filters on GPU-1 are colour agnostic
- Filters on GPU-2 are colour specific
Deep Networks
- > 10 layers: weight initialisation and batch normalization
- > 30 layers: skip connections
- > 100 layers: identity skip connections
Weight Initialization
- We want changes in the weights between layers to be around the same size.
- This is affected by the variance in input and output, number of outputs ($n_i^out$) and a constant that takes into account the transfer function ($G_0$)
- We know that for D layers, the variance is:
$Var[\frac{\delta}{\delta x}] = (\prod_{i=1}^D G_0 \times n_i^out\times Var[w^{(i)}])\times Var[\frac{\delta}{\delta z}]$
- We want the variance to be around the same between input and output (left and right) - so therefore we choose weights such that
$(\prod_{i=1}^D G_0 \times n_i^out\times Var[w^{(i)}]) = 1$
Batch Normalization
- We want to normalise the activations of the nodes of a particular layer. To do that, we normalise the activations $x_k^{(i)}$:
$\hat{x}_k^{(i)} = \frac{x_k^{(i)} - Mean[x_k^{(i)}]}{\sqrt{Var[x_k^{(i)}]}}$
- Then we shift and rescale it with our own custom mean and variance, that can be trained as well using backprop with the other parameters/weights.
$y_k^{(i)} = \beta_k^{(i)} + \gamma_k^{(i)}\times \hat{x}_k^{(i)}$
Residual Networks
- Skip a layer, add a skip connection and add to the output

- F(x) is called a residual component
- Corrects errors from previous layers, or provides additional details
- So instead of using H(x) as our output, we refine x with the residual F(x)
Dense Networks
- In a densely connected block, each layer is connected by shortcut connections to all preceding layers
- Each block is separeted by convolution and pooling
Texture Synthesis
- Pretrain CNN
- Hidden layers generated that are general purpose
- Pass input texture through CNN, compute feature map $F_{ik}^l$ for the $i^{th}$ filter at spatial location k in layer l
- Compute Gram matrix for each pair of features $G_{ij}^l = \sum_k F_{ik}^l \times F_{jk}^l$
- Feed random image into CNN, compute L2 distance between original and new image
- Backprop to get gradient on image pixels, update image and go to step 4
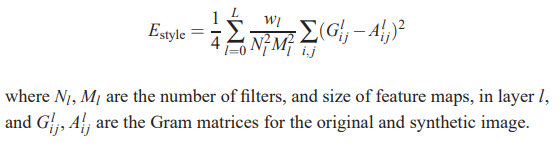
Neural Style Transfer
- Take content of image and style of another and combine to produce a new image
