Convolutional Networks
Convolutional Networks
Layers
- Convolution layers: extract shift-invariant features from the previous layer
- Subsampling/pooling layers: Combine activations of multiple units from previous layer into one unit
- Fully connected layers: Collect spatially diffuse information
- Output layer: Choose between classes
Softmax
Softmax extends the sigmoid function and allows you to classify $N$ classes, $z_j$ is the output corresponding to class $j$.
- Estimate is proportional to exponential
- All probabilities add to 1
- Normalise by dividing by sum
$P(i) = \frac{e(z_i)}{\sum_{j=1}^N e(z_j)}$
$log P(i) = z_i - log \sum_j exp(z_j)$
- First term pushes up the correct class $i$
- Second term pushes down the incorrect class $j$ with the highest activation
Convolutional
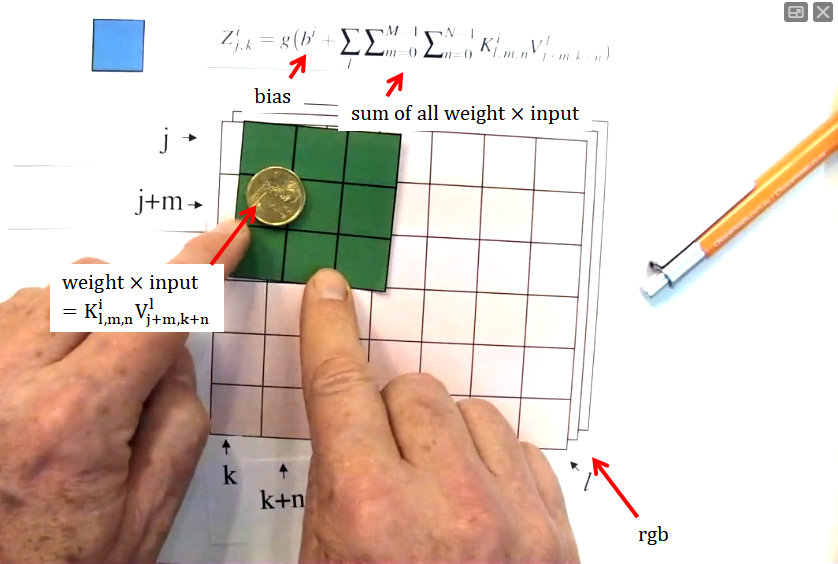
- 9 weights, the same weights are applied to each $M \times N$ block.
- Shift the green box (filter) along - because of the size of the filter, this will reduce the width and height of the next layer - becomes 5 by 4.
- If J=K=32, M=N=5, 3 input channels, 6 filters (different weights, detects different lines/features) in this layer:
- Width of next layer: 32 + 1 - 5 = 28
- Weights per neuron: 1 + 5 * 5 * 3 = 76
- includes bias, 5 * 5 weights, 3 input channels
- Neurons: 28 * 28 * 6 = 4704
- Number in the hidden layer
- Connections: weights * weights * neurons = 357,504
- Independent parameters: 6 * 76 = 456
- weights of each filter are independent
- Zero padding: treat off-edge inputs as zero, so it will be the same size of original image
- Stride dimensions: skipping some values (instead of 0, 1, 2… do 0, s, 2s…)
The other layers
- Max pooling:
- Get maximum value for pool of 4
- Stride is the number of neurons jumped
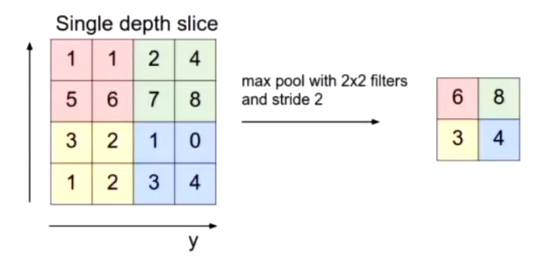
-
Overlapping pooling: when width is larger than stride
- Fully connected: layers connected and then passed through layers into output units