Geometry

Geometry

Encoder Networks

• Visualising hidden unit dynamics
• N-M-N task - e.g. 5-3-5 meaning 5 inputs, 5 outputs, squashing/bottleneck data into 3 hidden units

For N-2-N:

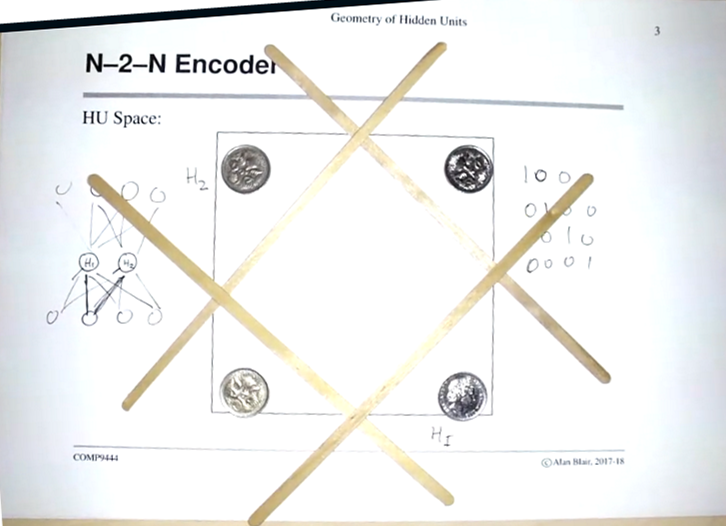
• This represents a 4-2-4 encoder.
  • There are 4 possible inputs that are the same as the outputs, represented by points. This is the table on the right.
  • There are two hidden units, which can be represented by lines (a function of H1, H2 and a bias).
  • The aim is for the hidden units to split the points (‘squash’ into two hidden units)
  • When there are too many inputs, the network becomes too constrained and unstable
• During training, the points start around the middle and move to the corners as it improves
• Similar to autoencoders that compress images, later in the course.
• If there are 3 hidden units, hidden units are not lines but planes, coins go to a corner of a square (e.g. for 8-3-8 it is coins on a cube octahedron)

Hinton Diagrams

• White is positive, black is negative, larger the point, the more positive/negative
• Looks at one hidden unit
• Superposition of inputs

Symmetries

• Swapping hidden nodes will have the same overall function
• Changing weights to be negative by reversing sign of weights
• If weights are the same for two hidden units, they will have the same errors and weight updates, which is why you should randomise your weights at the start
  • Hidden units should try to do a similar job first but then specialise
  • Each layer implements an approximately linear function, two layers introduces a bit of non-linearity. Should try not to be too non-linear

Limitations 2 Layer NN

• Twin Spirals
  • First layer is the line for positive/negative
  • Second layer learns convex features
  • Third layer can learn concave features, like holes
  • Hard to do - very low learning rate and initial weight values, otherwise network converges to local optimum
• https://www.cs.cmu.edu/~dst/pubs/byte-hiddenlayer-1989.pdf

Vanishing and Exploding Gradients

• When weights are too small, differentials become smaller as you backpropogate through the layers (exponentially, due to chain rule)
• When weights are too large, activations in higher layers saturate to extreme values - gradients also become very small
• Weights with intermediate values - differentials sometimes gets multiplied many times where the transfer function is steep - blow up
• Solved by:
  • Layerwise unsupervised training
    • Train and get useful features first before caring about the output
  • LSTM for recurrent neural networks
  • New activation functions

Dropout

• Medium article
• Drop out/ignore hidden and visible units in a neural network during training, when doing a forward/backward pass.
  • Nodes are dropped out with a probability 1-p.
  • After training, activations are multiplied by this probability - so activation is the average value of what it would have received.
• Redundancy - when features are missing
• Simulates ensembling - different classifiers trained on same task for more diversity
  • Diversity also achieved by training different subsets of data with replacement - some not chosen, some chosen multiple times
  • In dropout, this happens because it is different architecture (units) and then later averaged over all different models