Perceptrons

Neural Networks Introduction

  • Input edges with weights
  • Output edges with weights
  • Weights change over time
  • Nodes that receive input from other nodes and compute outputs. In a node:
    1. Nodes take a group of weighted inputs
    2. Add a bias weight
    3. Inputs are placed in an activation function, e.g. $g(s_i) = g(\sum_j(w_{ij}x_j))$
    4. Return an output

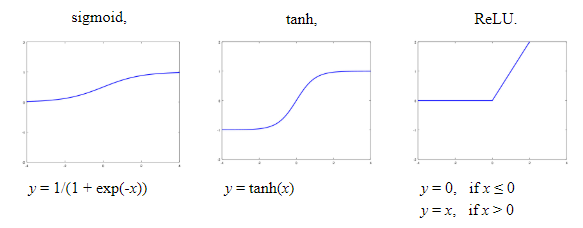
Activation Function

  • Also called transfer function
  • Can be used to introduce non-linear properties to the network
  • A ‘step’ from 0 to 1
  • Types:
    • sigmoid: $\sigma(x)=\frac{1}{(1+e^{-x})}$, from 0 to 1
    • tanh: $tanh(x)=\frac{2}{(1+e^{-2x})}-1$, from -1 to 1
    • ReLU: $f(x)=max(0, x)$, from 0 to x
    • Discontinuous step function
      • $g(x)=1$ if $x \geq 0$
      • $g(x)=0$ otherwise

Activations

Perceptrons

  • Perceptrons have two layers - input and output (single layer - one layer of links)
  • Activation function is the discontinuous step function
  • Can represent some boolean functions: AND, OR, NOR

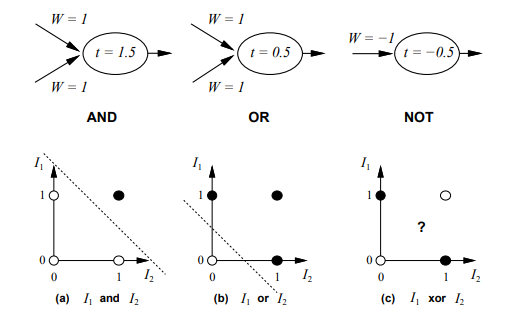
Boolean perceptrons, source https://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/15381-f01/www/handouts/110601.pdf

  • Cannot represent NOT - because it cannot be linearly separable

Perceptrons and Learning

Let $g(s)$ be the discontinuous step function.

For every input adjust the weights:

  • Error $E = y-g(x)$
  • Weights: $W_k \leftarrow W_k + \eta x_kE$

Where $\eta$ is the learning rate, $y$ is the correct output and $g(x)$ is the output of the network.

Good Resources